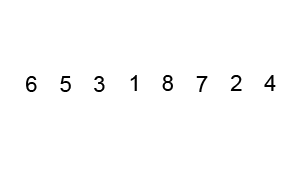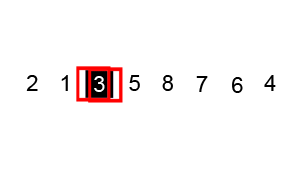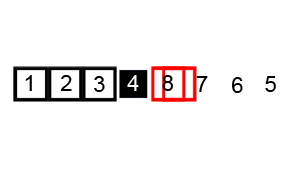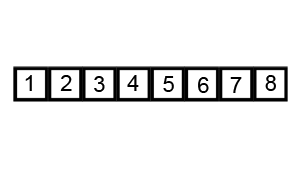Saheb Ghosh Reading time ~1 minute

Merge sort is one of the most effiecient Divide and Conquer Algorithm. This runs on Big-Oh(O)(nlogn) at worst case. Conceptually, a merge sort works as follows:

  • Divide the unsorted list into n sublists, each containing 1 element (a list of 1 element is considered sorted).
  • Repeatedly merge sublists to produce new sorted sublists until there is only 1 sublist remaining. This will be the sorted list.

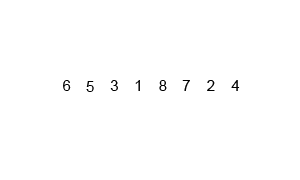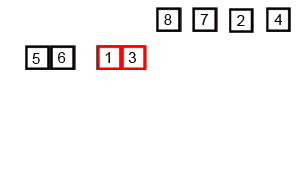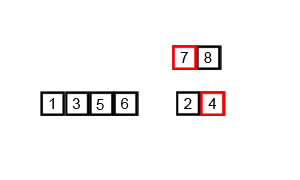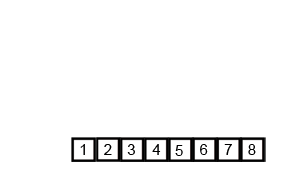
_config.yml

Program in C :

#include<stdio.h>
void mergesort(int a[],int i,int j);
void merge(int a[],int i1,int j1,int i2,int j2);
 
int main()
{
    int a[30],n,i;
    printf("Enter no of elements:");
    scanf("%d",&n);
    printf("\nEnter array elements:");
    
    for(i=0;i<n;i++)
        scanf("%d",&a[i]);
        
    mergesort(a,0,n-1);
    
    printf("\nSorted array is :");
    for(i=0;i<n;i++)
        printf("%d ",a[i]);
        
    return 0;
}
 
void mergesort(int a[],int i,int j)
{
    int mid;
        
    if(i<j)
    {
        mid=(i+j)/2;
        mergesort(a,i,mid);        //left recursion
        mergesort(a,mid+1,j);    //right recursion
        merge(a,i,mid,mid+1,j);    //merging of two sorted sub-arrays
    }
}
 
void merge(int a[],int i1,int j1,int i2,int j2)
{
    int temp[50];    //array used for merging
    int i,j,k;
    i=i1;    //beginning of the first list
    j=i2;    //beginning of the second list
    k=0;
    
    while(i<=j1 && j<=j2)    //while elements in both lists
    {
        if(a[i]<a[j])
            temp[k++]=a[i++];
        else
            temp[k++]=a[j++];
    }
    
    while(i<=j1)    //copy remaining elements of the first list
        temp[k++]=a[i++];
        
    while(j<=j2)    //copy remaining elements of the second list
        temp[k++]=a[j++];
        
    //Transfer elements from temp[] back to a[]
    for(i=i1,j=0;i<=j2;i++,j++)
        a[i]=temp[j];
}
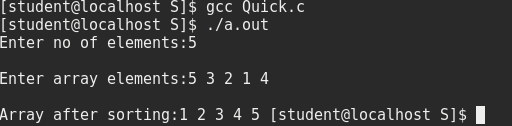
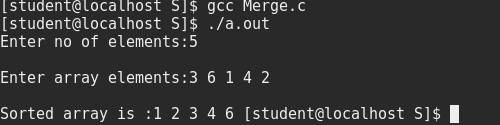
  • Output:

_config.yml

Please comment below in case of any problem found during running the code or any other doubts.

Saheb Ghosh Reading time ~1 minute

Quicksort is a divide and conquer algorithm. Quicksort first divides a large array into two smaller sub-arrays: the low elements and the high elements. Quicksort can then recursively sort the sub-arrays.

The steps are:

  • Pick an element, called a pivot, from the array.
  • Partitioning: reorder the array so that all elements with values less than the pivot come before the pivot, while all elements with values greater than the pivot come after it (equal values can go either way). After this partitioning, the pivot is in its final position. This is called the partition operation.
  • Recursively apply the above steps to the sub-array of elements with smaller values and separately to the sub-array of elements with greater values.

The base case of the recursion is arrays of size zero or one, which never need to be sorted. In asymptotic notation Quick sort can take upto O(n²) in wrost case , however on average its takes O(n log n).

The pivot selection and partitioning steps can be done in several different ways; the choice of specific implementation schemes greatly affects the algorithm’s performance. _config.yml

Program in C :

#include<stdio.h>
 
void quick_sort(int[],int,int);
int partition(int[],int,int);
 
int main()
{
    int a[50],n,i;
    printf("Enter no of elements:");
    scanf("%d",&n);
    printf("\nEnter array elements:");
    
    for(i=0;i<n;i++)
        scanf("%d",&a[i]);
        
    quick_sort(a,0,n-1);
    printf("\nArray after sorting:");
    
    for(i=0;i<n;i++)
        printf("%d ",a[i]);
    
    return 0;        
}
 
void quick_sort(int a[],int l,int u)
{
    int j;
    if(l<u)
    {
        j=partition(a,l,u);
        quick_sort(a,l,j-1);
        quick_sort(a,j+1,u);
    }
}
 
int partition(int a[],int l,int u)
{
    int v,i,j,temp;
    v=a[l];
    i=l;
    j=u+1;
do
    {
        do
            i++;
            
        while(a[i]<v&&i<=u);
        
        do
            j--;
        while(v<a[j]);
        
        if(i<j)
        {
            temp=a[i];
            a[i]=a[j];
            a[j]=temp;
        }
    }while(i<j);
    
    a[l]=a[j];
    a[j]=v;
    
    return(j);
}
  • Output:

_config.yml

Please comment below in case of any problem found during running the code or any other doubts.