Saheb Ghosh Reading time ~2 minutes

In a graph, a vertex is called an articulation point if removing it and all the edges associated with it results in the increase of the number of connected components in the graph. For example consider the graph given in following figure.

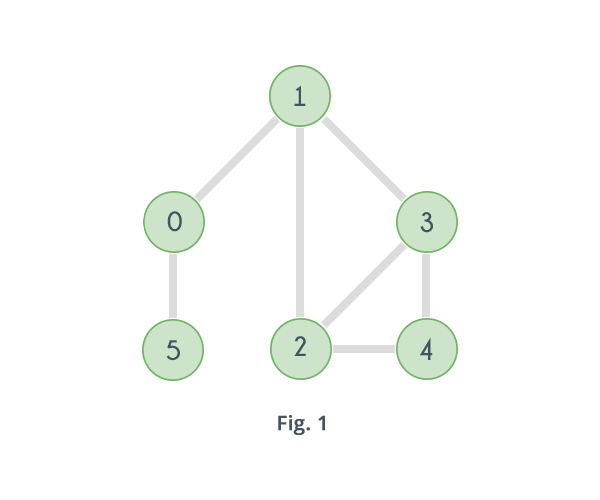
_config.yml

If in the above graph, vertex 1 and all the edges associated with it, i.e. the edges 1-0, 1-2 and 1-3 are removed, there will be no path to reach any of the vertices 2, 3 or 4 from the vertices 0 and 5, that means the graph will split into two separate components. One consisting of the vertices 0 and 5 and another one consisting of the vertices 2, 3 and 4 as shown in the following figure.

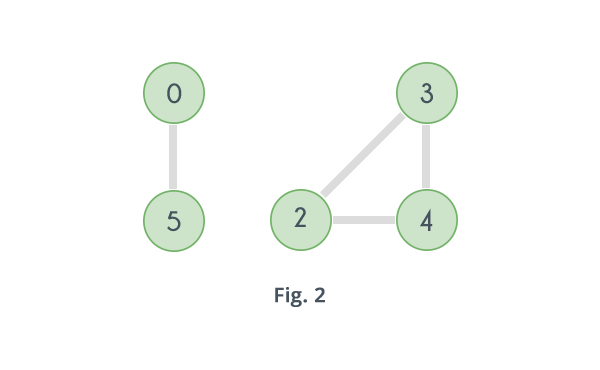
_config.yml

Likewise removing the vertex 0 will disconnect the vertex 5 from all other vertices. Hence the given graph has two articulation points: 0 and 1. Articulation Points represents vulnerabilities in a network.

Program in C :

#include<stdio.h>
#include<stdlib.h>
int min(int a,int b)
{
    return(a<b?a:b);
}
struct node
{
 int val;
 struct node* next;
};
struct graph
{   
 int v;
 struct node** arr;
};
struct graph* createGraph(int v)
{
    int i;
    struct graph* temp =(struct graph*)malloc(sizeof(struct graph));
    temp->v=v;
    for(i=0;i<v;i++)
     temp->arr=(int**)malloc(sizeof(int*)*v);
    for(i=0;i<v;i++)
     temp->arr[i]=NULL;
    return temp;
}
void addEdge(struct graph* g,int u,int v)
{
    struct node* temp =(struct node*)malloc(sizeof(struct node));
    temp->val = v;
    temp->next = g->arr[u];
    g->arr[u] = temp;     
}
void apUtil(struct graph * g,int node,int* isVisited,int* des,int* parent,int* low,int* ap)
{
    struct node* temp=NULL;
    static int time=0;
    int children=0;
    temp = g->arr[node];
    isVisited[node]=1;
    time++;
    //printf("\nsetting time for %d",node);
    des[node]=low[node]=time;

    while(temp!=NULL)
    {       
       if(!isVisited[temp->val])
        {
          children++;
          parent[temp->val]=node;
          apUtil(g,temp->val,isVisited,des,parent,low,ap);

      low[node]= min(low[node],low[temp->val]);

          if(parent[node]==-1 && children>1)
             ap[node]=1;

      if(parent[node]!=-1 && des[node]<=low[temp->val])
            ap[node]=1;           
        }    
        else if(temp->val!=parent[node])
        {
            low[node]=min(low[node],des[temp->val]);
        }
       temp= temp->next;
      }
     //printf("%d",node);
}
void AP(struct graph* g)
{
    int i;
    int* des = (int*)malloc(sizeof(int)*g->v);
    int* isVisited = (int*)malloc(sizeof(int)*g->v);
    int* parent = (int*)malloc(sizeof(int)*g->v);
    int* low = (int*)malloc(sizeof(int)*g->v);
    int* ap = (int*)malloc(sizeof(int)*g->v);
    for(i=0;i<g->v;i++)
    {
        isVisited[i]=0;
        parent[i]=-1;
        ap[i]=0;
    }
    for(i=0;i<g->v;i++)
    {
        if(isVisited[i]==0)
        {
            apUtil(g,i,isVisited,des,parent,low,ap);
        }
    }
    printf("\n");
    int flag=0;
    printf("Searching Articulation points ....");
    for(i=0;i<g->v;i++)
    {
       
        if(ap[i]==1)
	{
	  flag=1;
	  printf("\nVertex : %d",i);
	}
    }
    if(flag==0)
	printf("\nNo Articulation point found.");
}
void main()
{
    
    int size=0,edges=0,i,u,v;
    printf("Please enter size of the graph : ");
    scanf("%d",&size);
    printf("\nPlease number of edges : ");
    scanf("%d",&edges);
    struct graph* g = createGraph(size);
    for(i=0;i<edges;i++)
    {
	printf("\nEnter the edge %d\n",i);
  	scanf("%d %d",&u,&v);
	addEdge(g,u,v);
    }
    AP(g);
}

Output:

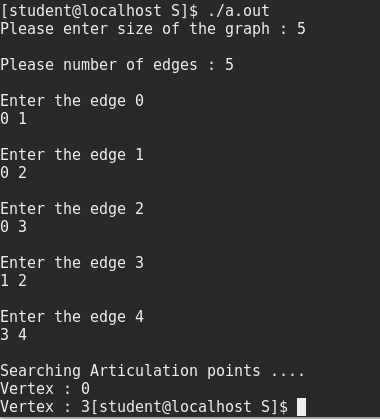
_config.yml

Please comment below in case of any problem found during running the code or any other doubts.

Saheb Ghosh Reading time ~2 minutes

Travelling Salesman Problem is defined as “Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?” It is an NP-hard problem.

Bellman–Held–Karp algorithm: Compute the solutions of all subproblems starting with the smallest. Whenever computing a solution requires solutions for smaller problems using the above recursive equations, look up these solutions which are already computed. To compute a minimum distance tour, use the final equation to generate the 1st node, and repeat for the other nodes. For this problem, we cannot know which subproblems we need to solve, so we solve them all.

_config.yml

Program in C :

#include <stdio.h>
int matrix[25][25], visited_cities[10], limit, cost = 0;
 
int tsp(int c)
{
 int count, nearest_city = 999;
 int minimum = 999, temp;
 for(count = 0; count < limit; count++)
 {
 if((matrix[c][count] != 0) && (visited_cities[count] == 0))
 {
 if(matrix[c][count] < minimum)
 {
 minimum = matrix[count][0] + matrix[c][count];
 }
 temp = matrix[c][count];
 nearest_city = count;
 }
 }
 if(minimum != 999)
 {
 cost = cost + temp;
 }
 return nearest_city;
}
 
void minimum_cost(int city)
{
 int nearest_city;
 visited_cities[city] = 1;
 printf("%d ", city + 1);
 nearest_city = tsp(city);
 if(nearest_city == 999)
 {
 nearest_city = 0;
 printf("%d", nearest_city + 1);
 cost = cost + matrix[city][nearest_city];
 return;
 }
 minimum_cost(nearest_city);
}
 
int main()
{ 
 int i, j;
 printf("Enter Total Number of Cities:\t");
 scanf("%d", &limit);
 printf("\nEnter Cost Matrix\n");
 for(i = 0; i < limit; i++)
 {
 printf("\nEnter %d Elements in Row[%d]\n", limit, i + 1);
 for(j = 0; j < limit; j++)
 {
 scanf("%d", &matrix[i][j]);
 }
 visited_cities[i] = 0;
 }
 printf("\nEntered Cost Matrix\n");
 for(i = 0; i < limit; i++)
 {
 printf("\n");
 for(j = 0; j < limit; j++)
 {
 printf("%d ", matrix[i][j]);
 }
 }
 printf("\n\nPath:\t");
 minimum_cost(0);
 printf("\n\nMinimum Cost: \t");
 printf("%d\n", cost);
 return 0;
}
  • Output:

_config.yml

Please comment below in case of any problem found during running the code or any other doubts.