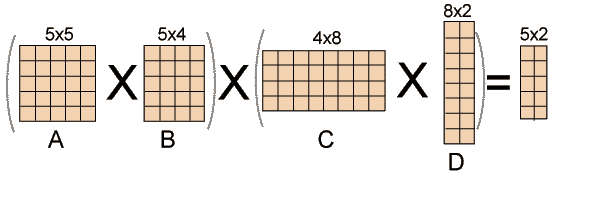
For a given source node in the graph, the algorithm finds the shortest path between that node and every other.It can also be used for finding the shortest paths from a single node to a single destination node by stopping the algorithm once the shortest path to the destination node has been determined. For example, if the nodes of the graph represent cities and edge path costs represent driving distances between pairs of cities connected by a direct road, Dijkstra’s algorithm can be used to find the shortest route between one city and all other cities. As a result, the shortest path algorithm is widely used in network routing protocols, most notably IS-IS (Intermediate System to Intermediate System) and Open Shortest Path First (OSPF). It is also employed as a subroutine in other algorithms such as Johnson’s.
Dijkstra’s Algorithm:
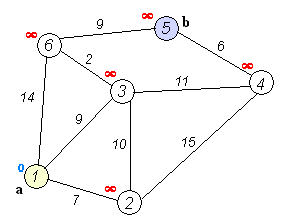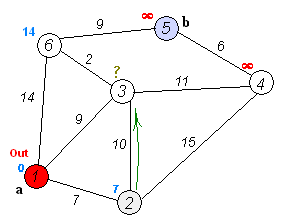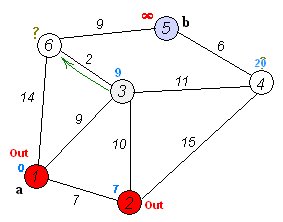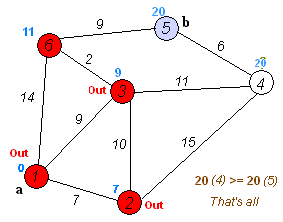
Let the node at which we are starting be called the initial node. Let the distance of node Y be the distance from the initial node to Y. Dijkstra’s algorithm will assign some initial distance values and will try to improve them step by step.
- Assign to every node a tentative distance value: set it to zero for our initial node and to infinity for all other nodes.
- Set the initial node as current. Mark all other nodes unvisited. Create a set of all the unvisited nodes called the unvisited set.
- For the current node, consider all of its neighbors and calculate their tentative distances. Compare the newly calculated tentative distance to the current assigned value and assign the smaller one. For example, if the current node A is marked with a distance of 6, and the edge connecting it with a neighbor B has length 2, then the distance to B (through A) will be 6 + 2 = 8. If B was previously marked with a distance greater than 8 then change it to 8. Otherwise, keep the current value.
- When we are done considering all of the neighbors of the current node, mark the current node as visited and remove it from the unvisited set. A visited node will never be checked again.
- If the destination node has been marked visited (when planning a route between two specific nodes) or if the smallest tentative distance among the nodes in the unvisited set is infinity (when planning a complete traversal; occurs when there is no connection between the initial node and remaining unvisited nodes), then stop. The algorithm has finished.
- Otherwise, select the unvisited node that is marked with the smallest tentative distance, set it as the new “current node”, and go back to step 3.
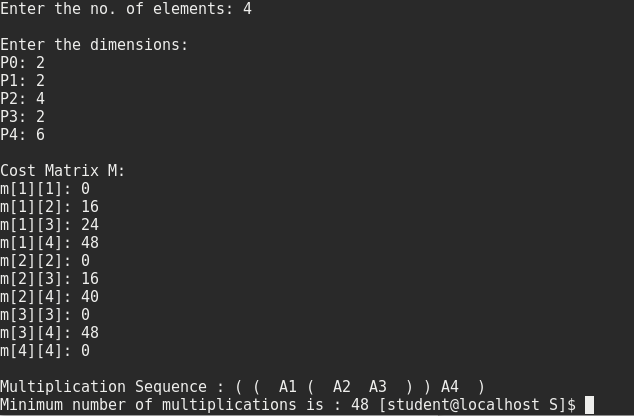
Program in C :
#include<stdio.h>
#define INFINITY 9999
#define MAX 10
void dijkstra(int G[MAX][MAX],int n,int startnode);
int main()
{
int G[MAX][MAX],i,j,n,u;
printf("Enter no. of vertices:");
scanf("%d",&n);
printf("\nEnter the adjacency matrix:\n");
for(i=0;i<n;i++)
for(j=0;j<n;j++)
scanf("%d",&G[i][j]);
printf("\nEnter the starting node:");
scanf("%d",&u);
dijkstra(G,n,u);
return 0;
}
void dijkstra(int G[MAX][MAX],int n,int startnode)
{
int cost[MAX][MAX],distance[MAX],pred[MAX];
int visited[MAX],count,mindistance,nextnode,i,j;
//pred[] stores the predecessor of each node
//count gives the number of nodes seen so far
//create the cost matrix
for(i=0;i<n;i++)
for(j=0;j<n;j++)
if(G[i][j]==0)
cost[i][j]=INFINITY;
else
cost[i][j]=G[i][j];
//initialize pred[],distance[] and visited[]
for(i=0;i<n;i++)
{
distance[i]=cost[startnode][i];
pred[i]=startnode;
visited[i]=0;
}
distance[startnode]=0;
visited[startnode]=1;#include<stdio.h>
#define INFINITY 9999
#define MAX 10
void dijkstra(int G[MAX][MAX],int n,int startnode);
int main()
{
int G[MAX][MAX],i,j,n,u;
printf("Enter no. of vertices:");
scanf("%d",&n);
printf("\nEnter the adjacency matrix:\n");
for(i=0;i<n;i++)
for(j=0;j<n;j++)
scanf("%d",&G[i][j]);
printf("\nEnter the starting node:");
scanf("%d",&u);
dijkstra(G,n,u);
return 0;
}
void dijkstra(int G[MAX][MAX],int n,int startnode)
{
int cost[MAX][MAX],distance[MAX],pred[MAX];
int visited[MAX],count,mindistance,nextnode,i,j;
//pred[] stores the predecessor of each node
//count gives the number of nodes seen so far
//create the cost matrix
for(i=0;i<n;i++)
for(j=0;j<n;j++)
if(G[i][j]==0)
cost[i][j]=INFINITY;
else
cost[i][j]=G[i][j];
//initialize pred[],distance[] and visited[]
for(i=0;i<n;i++)
{
distance[i]=cost[startnode][i];
pred[i]=startnode;
visited[i]=0;
}
distance[startnode]=0;
visited[startnode]=1;
count=1;
while(count<n-1)
{
mindistance=INFINITY;
//nextnode gives the node at minimum distance
for(i=0;i<n;i++)
if(distance[i]<mindistance&&!visited[i])
{
mindistance=distance[i];
nextnode=i;
}
//check if a better path exists through nextnode
visited[nextnode]=1;
for(i=0;i<n;i++)
if(!visited[i])
if(mindistance+cost[nextnode][i]<distance[i])
{
distance[i]=mindistance+cost[nextnode][i];
pred[i]=nextnode;
}
count++;
}
//print the path and distance of each node
for(i=0;i<n;i++)
if(i!=startnode)
{
printf("\nDistance of node%d=%d",i,distance[i]);
printf("\nPath=%d",i);
j=i;
do
{
j=pred[j];
printf("<-%d",j);
}while(j!=startnode);
}
}
count=1;
while(count<n-1)
{
mindistance=INFINITY;
//nextnode gives the node at minimum distance
for(i=0;i<n;i++)
if(distance[i]<mindistance&&!visited[i])
{
mindistance=distance[i];
nextnode=i;
}
//check if a better path exists through nextnode
visited[nextnode]=1;
for(i=0;i<n;i++)
if(!visited[i])
if(mindistance+cost[nextnode][i]<distance[i])
{
distance[i]=mindistance+cost[nextnode][i];
pred[i]=nextnode;
}
count++;
}
//print the path and distance of each node
for(i=0;i<n;i++)
if(i!=startnode)
{
printf("\nDistance of node%d=%d",i,distance[i]);
printf("\nPath=%d",i);
j=i;
do
{
j=pred[j];
printf("<-%d",j);
}while(j!=startnode);
}
}- Output:
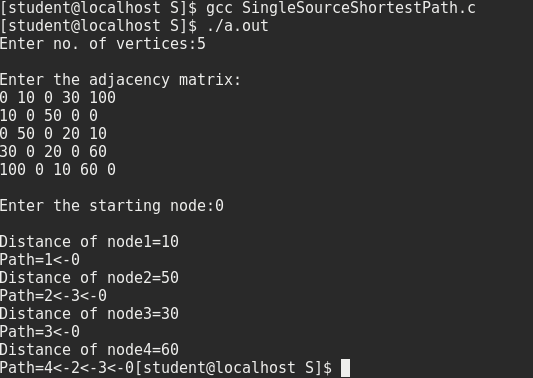
Please comment below in case of any problem found during running the code or any other doubts.