Welcome to Saheb's Blog

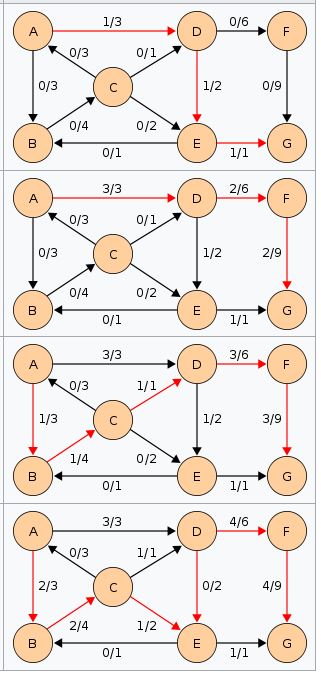
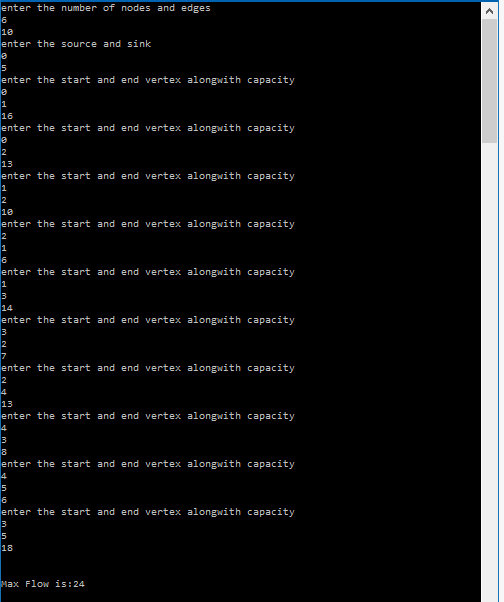
Kruskal’s algorithm

create a forest F (a set of trees), where each vertex in the graph is a separate tree

create a set S containing all the edges in the graph

while S is nonempty and F is not yet spanning

remove an edge with minimum weight from S
if the removed edge connects two different trees then add it to the forest F, combining two trees into a single tree

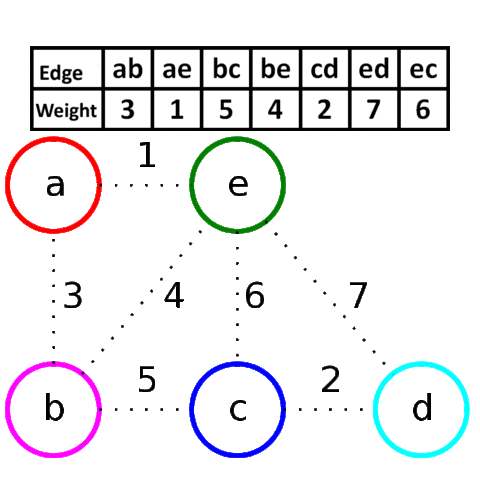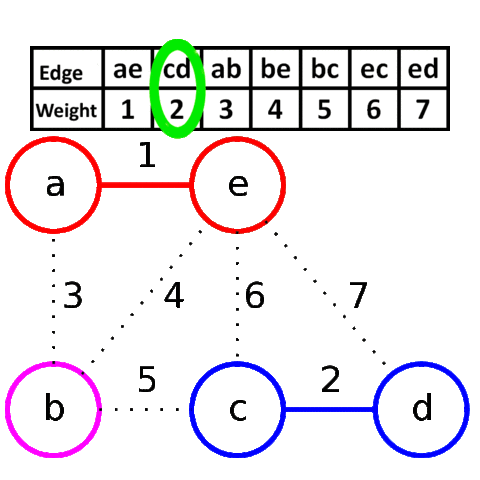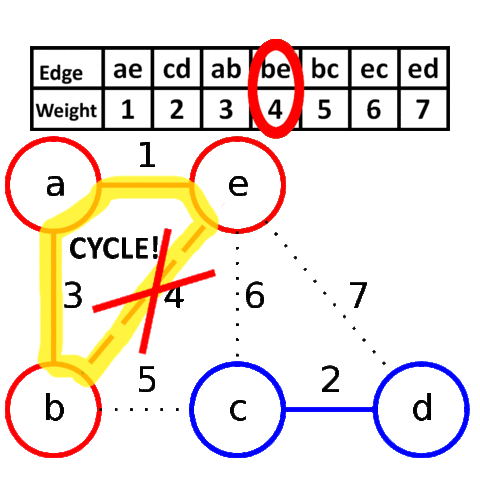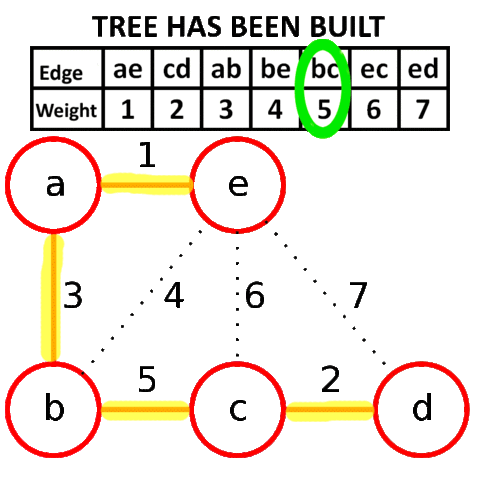
At the termination of the algorithm, the forest forms a minimum spanning forest of the graph. If the graph is connected, the forest has a single component and forms a minimum spanning tree Kruskal’s algorithm can be shown to run in O(E log E) time, or equivalently, O(E log V) time, where E is the number of edges in the graph and V is the number of vertices.

Program in C :

#include<stdlib.h>
#include<stdio.h>
 
#define NIL -1
#define MAX 100
 
struct edge
{
      int x;
      int y;
      int weight;
      struct edge *link;
}*front = NULL;
 
void create_tree(struct edge tree[]);
void insert_queue(int i, int j, int wt);
struct edge *delete_queue();
int isEmpty();
void make_a_graph();
 
int vertices;
 
int main()
{
      int count;
      struct edge tree[MAX];
      int tree_weight = 0;
      make_a_graph();
      create_tree(tree);
      printf("Edges in MST:\n");
      for(count = 1; count <= vertices - 1; count++)
      {
            printf("%d->", tree[count].x);
            printf("%d\n", tree[count].y);
            tree_weight = tree_weight + tree[count].weight;
      }
      printf("Total Weight of this Minimum Spanning Tree:\t%d\n", tree_weight);
      return 0;
}
 
void create_tree(struct edge tree[])
{
      struct edge *tmp;
      int y1, y2, root_y1, root_y2;
      int parent[MAX];
      int i, count = 0;
      for(i = 0; i < vertices; i++)
      {
            parent[i] = NIL;
      }
      while(!isEmpty( ) && count < vertices - 1) 
      {
            tmp = delete_queue();
            y1 = tmp->x;
            y2 = tmp->y; 
            while(y1 != NIL)
            {
                  root_y1 = y1;
                  y1 = parent[y1];
            }
            while(y2 != NIL)
            {
                  root_y2 = y2;
                  y2 = parent[y2];
            }
            if(root_y1 != root_y2)
            {
                  count++;
                  tree[count].x = tmp->x;
                  tree[count].y = tmp->y;
                  tree[count].weight = tmp->weight;
                  parent[root_y2] = root_y1;
            }
      }
      if(count < vertices - 1)
      {
            printf("Graph is Disconnected. Therefore, Spanning Tree is not possible\n");
            exit(1);
      }
}
 
void insert_queue(int i, int j, int wt)
{
      struct edge *tmp, *q;
      tmp = (struct edge *)malloc(sizeof(struct edge));
      tmp->x = i;
      tmp->y = j;
      tmp->weight = wt;
      if(front == NULL || tmp->weight < front->weight)
      {
            tmp->link = front;
            front = tmp;
      }
      else
      {
            q = front;
            while(q->link != NULL && q->link->weight <= tmp->weight)
            {
                  q = q->link;
            }
            tmp->link = q->link;
            q->link = tmp;
            if(q->link == NULL) 
            {
                  tmp->link = NULL;
            }
      }
}
 
struct edge *delete_queue()
{
      struct edge *tmp;
      tmp = front;
      front = front->link;
      return tmp;
}
 
int isEmpty()
{
      if(front == NULL)
      {
            return 1;
      }
      else
      {
            return 0;
      }
}
 
void make_a_graph()
{
      int count, weight, maximum_edges, origin_vertex, destination_vertex;
      printf("Enter Total Number of Vertices:\t");
      scanf("%d", &vertices);
      maximum_edges = vertices * (vertices - 1)/2;
      for(count = 0; count < maximum_edges; count++)
      {
            printf("Enter Edge [%d] Co-ordinates [-1 -1] to Quit\n", count + 1);
            printf("Enter Origin Point:\t"); 
            scanf("%d", &origin_vertex);
            printf("Enter Destination Point:\t");
            scanf("%d", &destination_vertex);
            if((origin_vertex == -1) && (destination_vertex == -1))
            {
                  break;
            }
            printf("Enter Weight for this Edge:\n");
            scanf("%d", &weight);
            if(origin_vertex >= vertices || destination_vertex >= vertices || origin_vertex < 0 || destination_vertex < 0)
            {
                  printf("Entered Edge Co - ordinates is Invalid\n");
                  count--;
            }
            else
            {
                  insert_queue(origin_vertex, destination_vertex, weight);
            }
      }
}

Edmonds–Karp algorithm is an implementation of the Ford–Fulkerson method for computing the maximum flow in a flow network in much more optimized approach. Edmonds-Karp is identical to Ford-Fulkerson except for one very important trait. The search order of augmenting paths is well defined. As a refresher from the Ford-Fulkerson wiki, augmenting paths, along with residual graphs, are the two important concepts to understand when finding the max flow of a network.

Edmonds–Karp algorithm

Augmenting paths are simply any path from the source to the sink that can currently take more flow. Over the course of the algorithm, flow is monotonically increased. So, there are times when a path from the source to the sink can take on more flow, and that is an augmenting path. This can be found by a breadth-first search, as we let edges have unit length. The running time of O(V E2) is found by showing that each augmenting path can be found in O(E) time, that every time at least one of the E edges becomes saturated (an edge which has the maximum possible flow), that the distance from the saturated edge to the source along the augmenting path must be longer than last time it was saturated, and that the length is at most V. Another property of this algorithm is that the length of the shortest augmenting path increases monotonically.

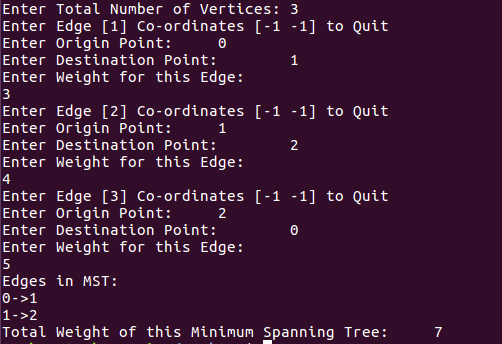
_config.yml

Notice how the length of the augmenting path found by the algorithm (in red) never decreases. The paths found are the shortest possible. The flow found is equal to the capacity across the minimum cut in the graph separating the source and the sink. There is only one minimal cut in this graph, partitioning the nodes into the sets { A , B , C , E } and { D , F , G } , with the capacity

c ( A , D ) + c ( C , D ) + c ( E , G ) = 3 + 1 + 1 = 5.

Program in C :

#include<cstdio>
#include<cstdio>
#include<queue>
#include<cstring>
#include<vector>
#include<iostream>
#include<conio.h>
using namespace std;
int capacities[10][10];

int flowPassed[10][10];

vector<int> graph[10];

int parentsList[10];       

int currentPathCapacity[10];  

 

int bfs(int startNode, int endNode)

{

    memset(parentsList, -1, sizeof(parentsList));

    memset(currentPathCapacity, 0, sizeof(currentPathCapacity));

 

    queue<int> q;

    q.push(startNode);

 

    parentsList[startNode] = -2;

    currentPathCapacity[startNode] = 999;

 

    while(!q.empty())

    {

        int currentNode = q.front();

        q.pop();

 

        for(int i=0; i<graph[currentNode].size(); i++)

        {

            int to = graph[currentNode][i];

            if(parentsList[to] == -1)

            {

                if(capacities[currentNode][to] - flowPassed[currentNode][to] > 0)

                {

                    parentsList[to] = currentNode;

                    currentPathCapacity[to] = min(currentPathCapacity[currentNode], 

                    capacities[currentNode][to] - flowPassed[currentNode][to]);

                    if(to == endNode)

                    {

                        return currentPathCapacity[endNode];

                    }

                    q.push(to);

                }

            }

        }

    }

    return 0;

}

 

int edmondsKarp(int startNode, int endNode)

{

    int maxFlow = 0;

      while(true)

    {

        int flow = bfs(startNode, endNode);

        if (flow == 0) 

        {

            break;

        }

        maxFlow += flow;

        int currentNode = endNode;

        while(currentNode != startNode)

        {

            int previousNode = parentsList[currentNode];

            flowPassed[previousNode][currentNode] += flow;

            flowPassed[currentNode][previousNode] -= flow;

            currentNode = previousNode;

        }

    }

    return maxFlow;

}
int main(){

    int nodesCount, edgesCount;

    cout<<"enter the number of nodes and edges\n";

    cin>>nodesCount>>edgesCount;
    int source, sink;

    cout<<"enter the source and sink\n";

    cin>>source>>sink;

    for(int edge = 0; edge < edgesCount; edge++)

    {
        cout<<"enter the start and end vertex alongwith capacity\n";

        int from, to, capacity;

        cin>>from>>to>>capacity;

 

        capacities[from][to] = capacity;

        graph[from].push_back(to);

 

        graph[to].push_back(from);

    }
    int maxFlow = edmondsKarp(source, sink);
    cout<<endl<<endl<<"Max Flow is:"<<maxFlow<<endl;
    getch();
}

Output:

_config.yml

Please comment below in case of any problem found during running the code or any other doubts.

Posts

Categories

Tags

Home

Welcome to Saheb's Blog

Minimum spanning tree-Kruskal's algorithm, with C Program Example

Kruskal’s algorithm

Program in C :

Output:

Maximum flow problem - Edmonds–Karp algorithm, with C Program Example

Edmonds–Karp algorithm

Program in C :

Output: