The Ford-Fulkerson algorithm is a method that resolves the max-flow min-cut problem. That is, given a network with vertices and edges between those vertices that have certain weights, how much “flow” can the network process at a time? Flow can mean anything, but typically it means data through a computer network. When the capacities are integers, the runtime of Ford–Fulkerson is bounded by O ( E *f ).
Ford-Fulkarson’s algorithm
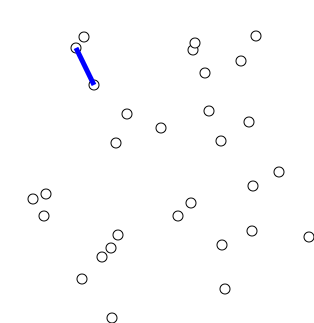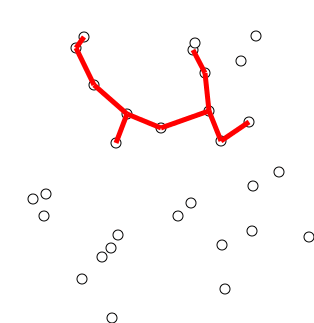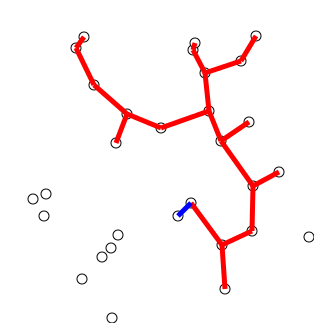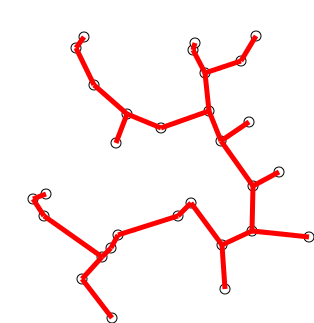
Given a graph which represents a flow network where every edge has a capacity. Also given two vertices source ‘s’ and sink ‘t’ in the graph, find the maximum possible flow from s to t with following constraints:
- Flow on an edge doesn’t exceed the given capacity of the edge.
- Incoming flow is equal to outgoing flow for every vertex except s and t.
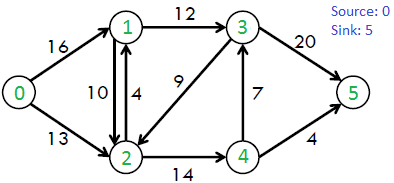
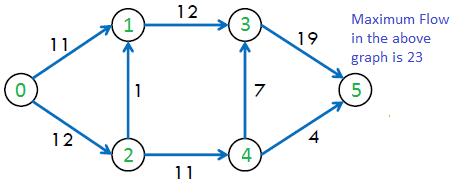
The maximum possible flow in the above graph is 23.
Program in C :
#include <stdio.h>
#define WHITE 0
#define GRAY 1
#define BLACK 2
#define MAX_NODES 1000
#define oo 1000000000
int n; // number of nodes
int e; // number of edges
int capacity[MAX_NODES][MAX_NODES]; // capacity matrix
int flow[MAX_NODES][MAX_NODES]; // flow matrix
int color[MAX_NODES]; // needed for breadth-first search
int pred[MAX_NODES]; // array to store augmenting path
int min (int x, int y) {
return x<y ? x : y; // returns minimum of x and y
}
int head,tail;
int q[MAX_NODES+2];
void enqueue (int x) {
q[tail] = x;
tail++;
color[x] = GRAY;
}
int dequeue () {
int x = q[head];
head++;
color[x] = BLACK;
return x;
}
int bfs (int start, int target) {
int u,v;
for (u=0; u<n; u++) {
color[u] = WHITE;
}
head = tail = 0;
enqueue(start);
pred[start] = -1;
while (head!=tail) {
u = dequeue();
// Search all adjacent white nodes v. If the capacity
// from u to v in the residual network is positive,
// enqueue v.
for (v=0; v<n; v++) {
if (color[v]==WHITE && capacity[u][v]-flow[u][v]>0) {
enqueue(v);
pred[v] = u;
}
}
}
// If the color of the target node is black now,
// it means that we reached it.
return color[target]==BLACK;
}
int max_flow (int source, int sink) {
int i,j,u;
// Initialize empty flow.
int max_flow = 0;
for (i=0; i<n; i++) {
for (j=0; j<n; j++) {
flow[i][j] = 0;
}
}
// While there exists an augmenting path,
// increment the flow along this path.
while (bfs(source,sink)) {
// Determine the amount by which we can increment the flow.
int increment = oo;
for (u=n-1; pred[u]>=0; u=pred[u]) {
increment = min(increment,capacity[pred[u]][u]-flow[pred[u]][u]);
}
// Now increment the flow.
for (u=n-1; pred[u]>=0; u=pred[u]) {
flow[pred[u]][u] += increment;
flow[u][pred[u]] -= increment;
}
max_flow += increment;
}
// No augmenting path anymore. We are done.
return max_flow;
}
void read_input_file() {
int a,b,c,i,j;
FILE* input = fopen("data.txt","r");
// read number of nodes and edges
fscanf(input,"%d %d",&n,&e);
printf("\nNumber of Vertices : %d Edges : %d",n,e);
// initialize empty capacity matrix
for (i=0; i<n; i++) {
for (j=0; j<n; j++) {
capacity[i][j] = 0;
}
}
// read edge capacities
for (i=0; i<e; i++) {
fscanf(input,"%d %d %d",&a,&b,&c);
capacity[a][b] = c;
printf("\nA : %d B : %d Capacity : %d",a,b,c);
}
fclose(input);
}
int main () {
read_input_file();
printf("\nPlease enter Source(s) and Sink(t) :\n");
int s=0,t=n-1;
scanf("%d %d",&s,&t);
printf("\nMax Flow : %d\n",max_flow(s,t));
return 0;
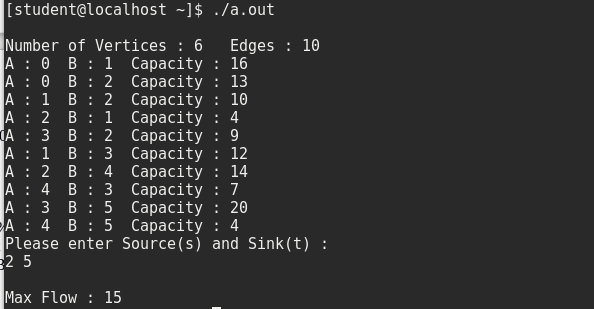
}Output:
Please comment below in case of any problem found during running the code or any other doubts.